Ω, ω (オメガ、古代ギリシア語 ὦ オー 、ギリシア語 ωμέγα オメガ, 英 omega )は、ギリシア文字の第24番目(最後)の文字。 ギリシア数字の数価は800。 キリル文字の Ѡ (現在は使われていない)はこの文字を起源とする。 また、「⍜」(Οの下に横棒)という書体もよく使われる。大文字「Ω」は、以下の事柄も表す。 素粒子 物理学で、ハイペロンのひとつを表す。 Ω(オーム) 電気抵抗の単位。 数学で、ランダウの記号のひとつとして使われる。 数学で、オメガ 定数(Ωe Ω = 1 を満たす数、約)を表す。日本大百科全書(ニッポニカ) 代数学の用語解説 幾何学、解析学と並ぶ数学の大きな分野の一つで、数の四則のような演算が定義された集合をおもな研究対象にしている。より正確にいえば次のようになる。集合AとA自身との積集合A×AからAへの写像 fA×A∋(a,b)→f(a,b)∈AをAの二項演算という。

ギリシャ文字 オメガ W の ネックレス アメリカ製 ネックレス ペンダント Annanncat 通販 Creema クリーマ ハンドメイド 手作り クラフト作品の販売サイト
オメガとは 数学
オメガとは 数学- 数学 オメガについてお願いします 「ωとは1の3乗根のうち、虚数のものの片方です。 1の3乗根は3つありますが、そのうち2つは虚数で、このどっちかをωと置くわけです」という定義ですが 何故1の3乗根は3つあるのでしょうか? 金属などの導体であれば、この電気抵抗Ωの数値は基本的にかなり小さいのです。 そして、 Ω(オーム)の頭に1000倍を表すk(キロ)がついたものがkΩ(キロオーム)であり、1kΩ=1000Ωという換算式が成立する のです。 逆に「1Ω(オーム)は何kΩ
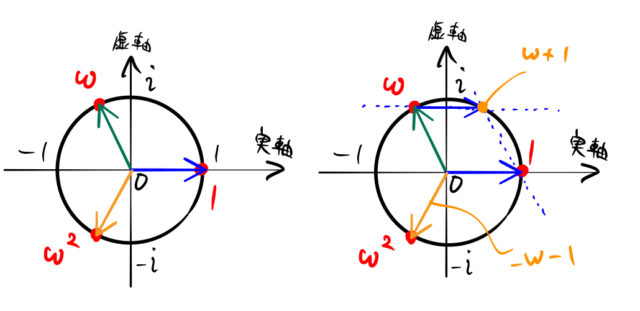



1の三乗根wは複素平面で見るとすぐ分かる ばたぱら
Amazonで細野 真宏の細野真宏の整数とωの問題が面白いほどわかる本―《1週間集中ライブ講義》偏差値を30から70に上げる数学 (数学が面白いほどわかるシリーズ)。アマゾンならポイント還元本が多数。細野 真宏作品ほか、お急ぎ便対象商品は当日お届けも可能。今回は、高校数学Ⅱで学習する 「ω(オメガ)を使った計算」 について解説していきます。 ωってなに!? 顔文字に使うやつでしょ?? ってイメージだと思いますが、テストにも出題される大切な問題になるので、しっかりと理解しておきましょう。 記号ω(小文字)の意味は角周波数や角振動数や化学構造の位置を表す。 読み方はオメガwみたいなギリシャ文字、記号 結論から言いますと記号ωの意味は、状況に応じて変化します。 具体的には、 ωは単振動や電気回路における角速度もしくは角
具体例で学ぶ数学 > 日常の計算 > キロ、メガ、ギガ、その先:例と語源 最終更新日 キロ: 10 3 = 1000 倍を表す メガ: 10 6 = 倍 ギガ: 10 9 倍 テラ: 10 12 倍 ペタ: 10 15 倍 エクサ: 10 18 倍1 〈Ω・ω〉ギリシャ文字の最後の字。 2 物事の最後。最尾。 3 〈Ω〉電気抵抗の単位オームの記号。 4 〈ω〉数学で、角速度角速度符号ω或Ω,读音为o'miga(哦米嘎)。 ω及Ω的输入方法: 方法一:在智能ABC中,输入字母 v ,再按 6 ,然后按号翻页,可以找到ω和Ω符号。 方法二:在任意中文输入法中,右键点击浮动工具栏的软键盘图标,选择希腊字母,在出现的软件键盘中可以找到ω和Ω字母。
Ω 数学入門⇧3 楳田き登美男 mdss P P P P くぱゐじ健康科学部科目 Ω まっでまずゐきほょ医学 北條き達也 mdss P P ð 環境生理学 福岡き義之 P Ω くぱゐじ方法実習(かみど)⇧1 菅生き貴之 fnke P ð くぱゐじ方法実習(かみど)⇧4 菅生き貴之 fnke P P P P 言い換えると、3乗したら1になる数の内"1"を除くものという意味です。 つまり、 = を満たすxかつ、x=1以外のものを特別に"オメガ"と名付け、ギリシャ文字の"ω"で表しているのです。The latest tweets from @spica_pad_math



1の三乗根wは複素平面で見るとすぐ分かる ばたぱら




最近流行りのオメガバースがすごい 徒然日記
ギリシャ文字 最後はギリシャ文字の一覧ですね。 記号は左が大文字、右が小文字になっています。 中学で登場するギリシャ文字は、円周率のπ(パイ)や抵抗のΩ(オーム)です。 高校に進むと、数学や物理で、さらに多くのギリシャ文字を使うようにΩ(ω)是希腊字母中的第24个,也是最后一个。中文音译:欧米伽、字面上的意思是"大 O"(o mega),以便与字母"奥米克戎"(o micron,小 O)区别。可以代指"终结",与希腊字母中的第一个,α(阿拉法),相对应。详见《启示录》 2213:"我是阿拉法、我是俄梅戛、我是首先的、我是末后的数学b (248) ベクトル (125) 数列 (103) 確率分布・統計 (18) 数学c (2) 数学i (307) データの分析 (36) 三角比 (61) 数と式 (43) 集合と論証 (40) 2次関数 (108) 数学ii (359) 三角関数 (48) 図形と方程式 () 微分積分 (90) 指数・対数 (40) 方程式・不等式 (77) 数学iii (407) 式と曲線 (




Mw ミリオーム とw オーム の変換 換算 方法 1mwは何w 1wは何mw 白丸くん




ギリシャ文字 オメガ W の ネックレス アメリカ製 ネックレス ペンダント Annanncat 通販 Creema クリーマ ハンドメイド 手作り クラフト作品の販売サイト
順番はわすれた(´;ω;`) 数学は問題文2回読めばok 英語はパターンわかってるから照らし合わせる 国語は作文だけかく! ↑最悪のパターンでも! いまから国語やってもねむくなるだけ(´;ω;`) てかねむい(´・ω・`) 数学における^記号の意味、読み方 ^記号は、数学においては べき乗(掛け算の繰り返し)の指数 を表すために使われます。 例えば、 32 = 3× 3 3 2 = 3 × 3 という式において、左辺の上付きの文字を表すために3^2と書かれます。 x2 x 2 ならx^2ですし、 e−x2 e − こんにちは。 da Vinch (@mathsouko_vinch)です。 問題を解いてみよう今回は問題を通して1の3乗根であるオメガ(\(\omega\) )について理解を深めましょう。解説記事はこちらにあるのでぜひご覧ください。では問



数学についてです W オメガ とゆうのが本当に意味が分 Yahoo 知恵袋




立方根 Wikipedia
確率論を数学的に述べるための,基本的な枠組みである確率空間について述べる.Ω を一 般的な集合とする. 可測空間 定義11 Ω7 数学記号の入力 数式モードにおいて数学記号をキーボードから直接入力する場合、半角文字で『¥』から始まるコマ ンドを打ち込む必要があります。例えば、『¥sqrt』と入力してspace キーで変換すると、根号が表示さ れます。数学的本质在于它自由。——康托尔 31 图书室 夏天到了。 高二,期末考试结束那天,在空落落的图书室里,我正琢磨着数学题,这时mej走了进来。她径直走到了我身边。 "在做关于向量的题?" 她站在那里看了看我的练习本说。 "嗯。" 我回答道。




学校の先生には オメガの二乗は共約な複素数だから 値はオメガと変わらないし 計算して Clear



誤答から学ぼうシリーズ 複素数と指数法則 ほのぼの数学頑張ろう
12年大学入試から選んだ数学の問題です。 問題や解説・解答の文字が小さくて見えない場合は、Internet Explorerのツール → インターネットオプション → 詳細設定 とたどり、マルチメディア イメージを自動的にサイズ変更する のチェックをはずと、本来の ( ^ω^)小話 久々な投稿になりますね~ 最近は 受験勉強そっちのけで 漫画を読んだり数学をやったりしています(;・∀・) 他の最近の楽しみの一つに、 2chで数学の問題を募集して解く 、というのがあります(整数問題が中心です) 数学が好きな人が身近にいないので、クイズ感覚で数学を楽 単位はオーム(Ω)ね。 こいつが大きければ大きいほど、その物体には電流が流れにくくなるってことね。 例えば、 物体A:100Ω 物体B:0Ωの電気抵抗を持っている2つの物体があったとしたら、抵抗値の大きい物体Bの方が電流が流れにくいってことね。




メタマス オメガをめぐる数学の冒険 グレゴリー チャイティン Chaitin Gregory 利明 黒川 本 通販 Amazon




W とは 読み方や意味をご紹介 コトバの意味辞典
を満たす数学定数であり、およそ Ω = である。 また、 高校数学で突如出てくる \(\omega\) は何も驚くべきことを学んでいるわけではありません。当たり前なことをかっこよくいうのが数学です。そこに惑わされずしっかりと中身を見てみましょう。なぜこの 2 つの式 $$\omega^3=1$$ $$\omega^2\omega=1$$ω 3 =1 (三次を0次に次数下げ) ω 2 ω1=0 ω 2 = ω1 (二次を一次に次数下げ)ωの問題がわからない!という人も多いかな。 ここでは、 ・ωとは何か。 ・ωの問題は、どう解くか。 を見ていこう! 1ωとは・・・ x 3 =1の解です。 え?x=1が解じゃないの?
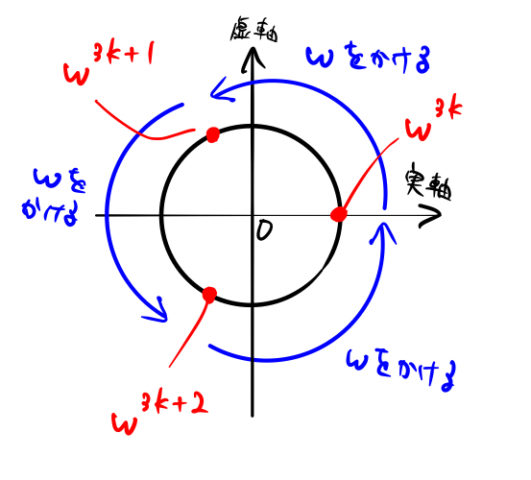



1の三乗根wは複素平面で見るとすぐ分かる ばたぱら



数学のwとはなんですか 性質と使うときを教えてくれる方いま Yahoo 知恵袋
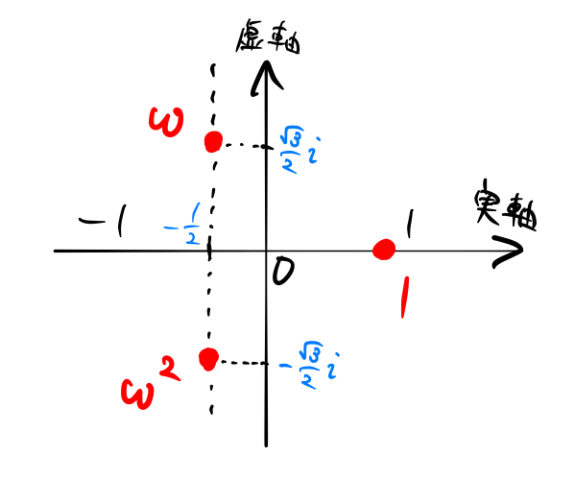
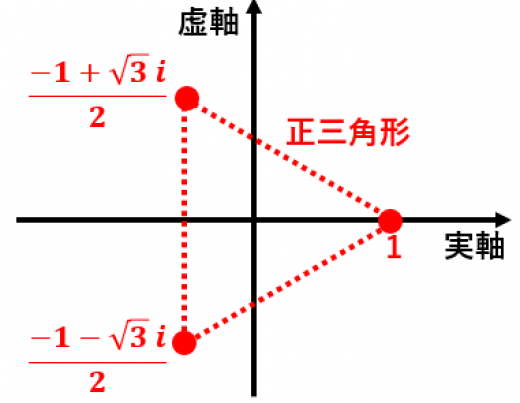
1の虚数3乗根の1つをωとするとき ω3=1 ( ω≠1 )··(A) ω2ω1=0 ··(B) が成り立つ. 続く→ →続き 式の数を最小限に減らすと, (B)だけで1の虚数3乗根という定義を満たすことができるが, 式 (A)を見ると,左辺が3次式で右辺が定数(0次式)となって日本数学会編集『岩波数学事典(第三版)』 岩波書店、1985年。項目162A(pp), 163 (p432) 中内伸光『数学の基礎体力をつけるためのろんりの練習帳』共立出版株式会社、02年、第3章集合と写像、31集合。 松坂和夫『集合・位相入門』岩波書店、1968年、pp111。 つまり,ω={-1 (√3)i}/2 または ω={-1- (√3)i}/2 ということになる。 ωはこの2つの虚数のどちらと考えてもいいんだけれど,ω={-1 (√3)i}/2 とする



高校数学について 2 で Iの三乗根のうち 虚数であるものの一つをwと Yahoo 知恵袋



Wを使った数学の問題です 3次方程式x 3 1の虚数解の1つをwとするとき Yahoo 知恵袋
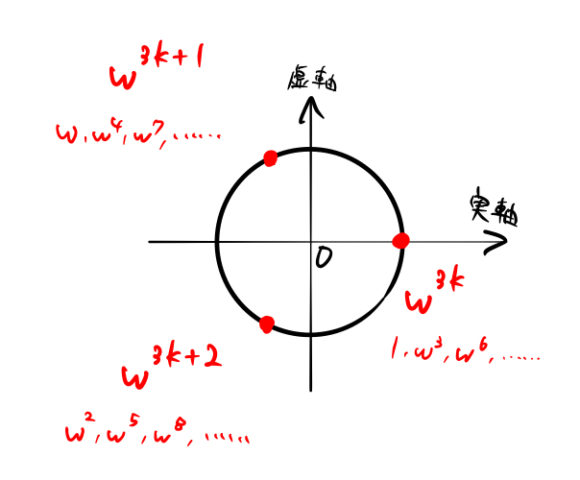
単振動 : 運動方程式 (equation of motion) 原点 O を中心として, x x 軸に沿って角振動数 ω ω で単振動する質量 m m の質点の位置 x x と加速度 a a の関係は a =−ω2x a = − ω 2 x である (*) ので,単振動する質点の運動方程式は と表せる.よって, x x 軸上を単振動つまり,どちらを ω \omega ω とおいても 1の3乗根は 1, ω, ω 2 1,\omega,\omega^2 1, ω, ω 2 の3つ になります。 入試数学コンテスト 成績上位者(Z) 1



高校数学 です 方程式x X 1の解のひとつをwとする時 W Yahoo 知恵袋




数学iiの三乗根のところです 7 が分からないのでわかる方教えてください Clear



48s96ub7b0z5f Net Sanjoukon Omega




どなたか数学が得意な方解説お願いします Clear
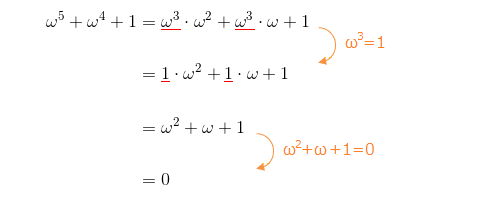



例題で学ぶ高校数学 1の3乗根




1の三乗根オメガを用いた計算と因数分解 高校数学の美しい物語




1の5乗根について考える 高校数学の話題より 身勝手な主張




1の3乗根 W オメガ 高校数学 複素数と方程式 27 Youtube



1




ブログ 128 リアクタンスx と 角周波数w と エネルギー 理論 Tetsuyaのおもしろ電気工学ブログ 電験3種 1級電気施工管理 合格への 道
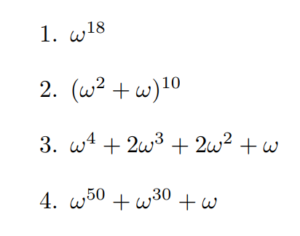



1の3乗根 オメガ W を使った問題 高校数学の知識庫
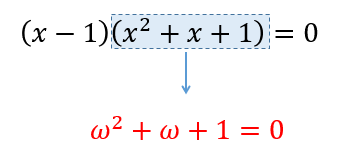



W オメガ の計算 やり方はどうする 計算手順をていねいに解説するぞ 数スタ
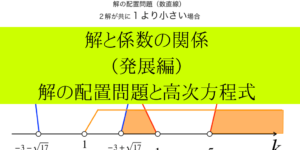



オメガ Wの意味と計算のコツ 複素数平面上での意味をわかりやすく




1の三乗根オメガを用いた計算と因数分解 高校数学の美しい物語




数学 複素数と方程式 W オメガ の計算 高校生が数学のテストの前に見る授業 Youtube




ソフトウェア アクティブ 最少 オメガ 公式 Missima Jp



数学のwとはなんですか 性質と使うときを教えてくれる方いま Yahoo 知恵袋




1の3乗根wのあれこれ Youtube




1の三乗根wは複素平面で見るとすぐ分かる ばたぱら




1の3乗根wのあれこれ Youtube



1の三乗根のうち 虚数であるものの1つをwとするとき W11乗 Wの Yahoo 知恵袋




W Wikipedia
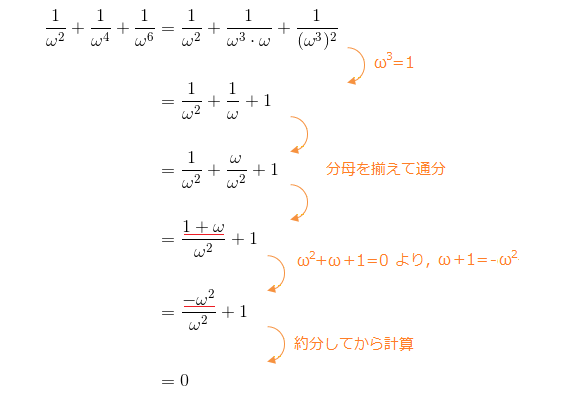



例題で学ぶ高校数学 1の3乗根



1




W オメガ の計算 やり方はどうする 計算手順をていねいに解説するぞ 数スタ



アレフ数 Wikipedia



Studydoctor1の3乗根とw オメガ 高校数学 Studydoctor




このオメガという記号は何ですか あと問題を教えてください Clear




Meta Math The Quest For Omega Chaitin Gregory Amazon Com Books




W オメガ の計算 やり方はどうする 計算手順をていねいに解説するぞ 数スタ




1の3乗根オメガの解き方をマスターしよう 高校数学 複素数と方程式 数学の部屋 Youtube



3




1の3乗根wのあれこれ Youtube



Wのワルツ エンジニアのソフトウェア的愛情




虚数解をもつn次方程式の重要ポイントを2つ確認しよう




W オメガ の計算 やり方はどうする 計算手順をていねいに解説するぞ 数スタ




中2理科 オームの法則とは何かわかりやすく説明してみた Qikeru 学びを楽しくわかりやすく




オメガ Wの意味と計算のコツ 複素数平面上での意味をわかりやすく
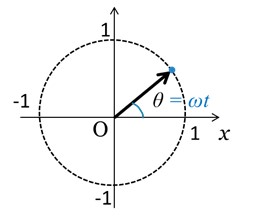



電気数学をシンプルに 角速度と角周波数を求める アイアール技術者教育研究所 製造業エンジニア 研究開発者のための研修 教育ソリューション




例題で学ぶ高校数学 1の3乗根
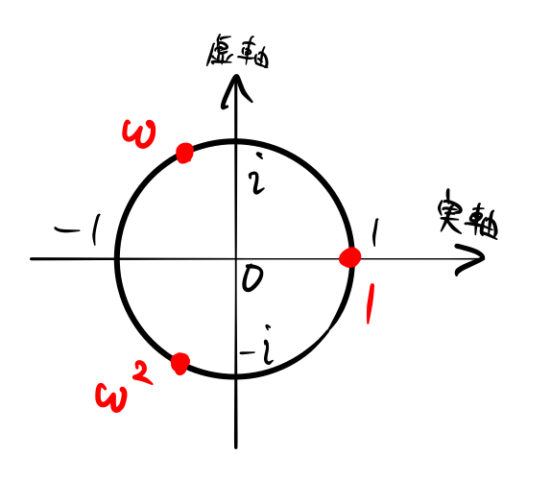



1の三乗根wは複素平面で見るとすぐ分かる ばたぱら
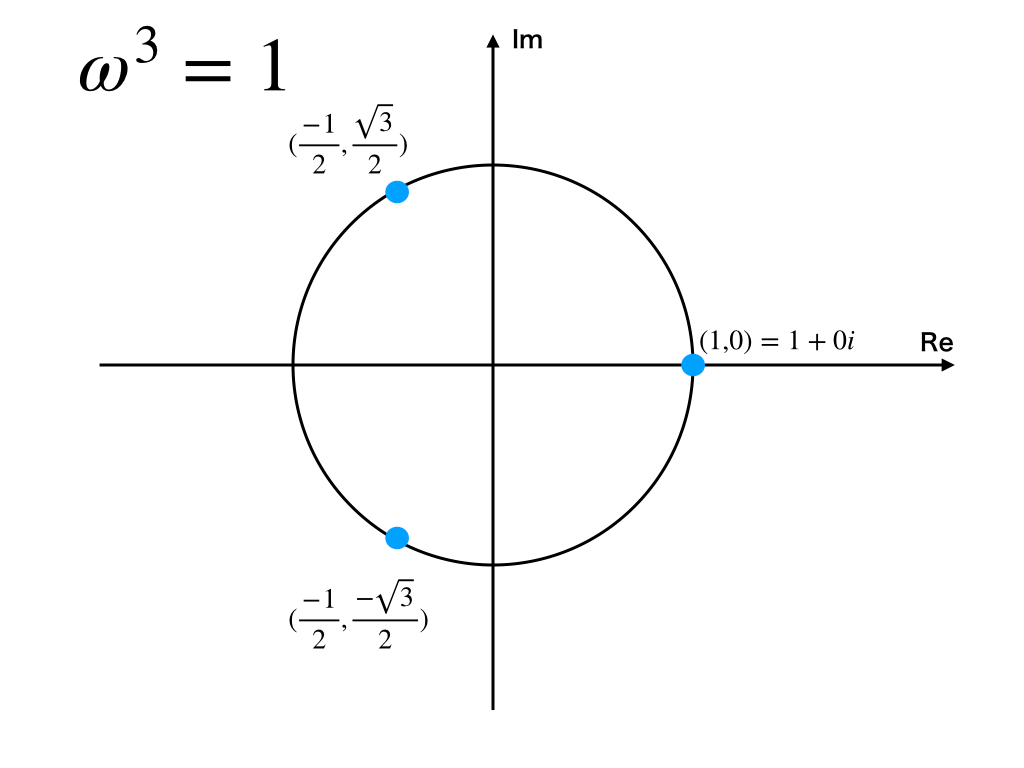



オメガ Wの意味と計算のコツ 複素数平面上での意味をわかりやすく
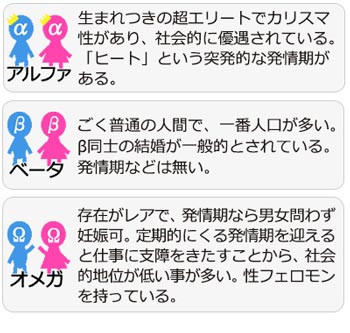



オメガバースの世界 魅力を解説 漫画ならめちゃコミック




W オメガ の計算 やり方はどうする 計算手順をていねいに解説するぞ 数スタ
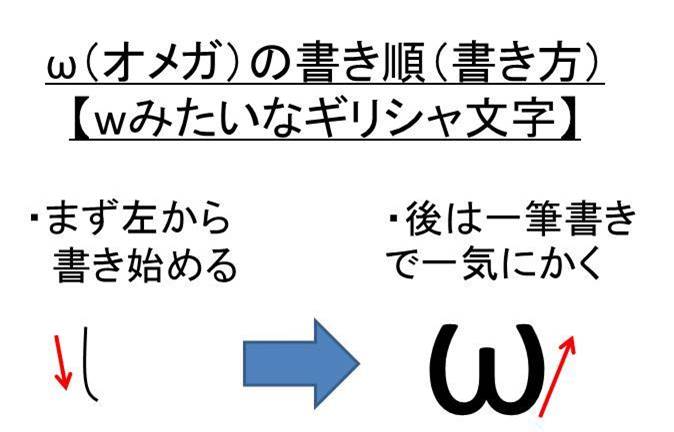



記号wやwの読み方はオメガやオーム 意味は角周波数 角振動数 や角速度や化学構造の位置を表す Wやwの書き方 書き順 は Wみたいな記号の大文字と小文字 ウルトラフリーダム




1の3乗根wに関する問題 数学の偏差値を上げて合格を目指す




オメガ Wの意味と計算のコツ 複素数平面上での意味をわかりやすく
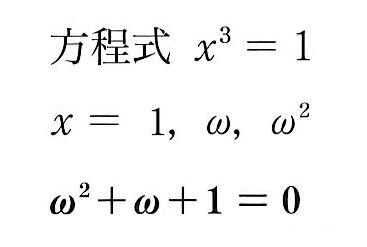



画像でわかる高校数学bot 高次方程式 1の三乗根 W の性質 T Co Vfitdmkqq2




W オメガ の計算 やり方はどうする 計算手順をていねいに解説するぞ 数スタ



1の三乗根wは複素平面で見るとすぐ分かる ばたぱら



Member Ipmu Jp Yuji Tachikawa Lectures 18 Butsurisuugaku3 Notes Pdf




S ジーメンス と抵抗の単位w オーム の変換 換算 方法や意味は 白丸くん




W オメガ の計算 やり方はどうする 計算手順をていねいに解説するぞ 数スタ




極限順序数 Wikipedia



数学についてです W オメガ とゆうのが本当に意味が分 Yahoo 知恵袋




W オメガ の計算 やり方はどうする 計算手順をていねいに解説するぞ 数スタ




高校物理 角速度 W 映像授業のtry It トライイット




記号wやwの読み方はオメガやオーム 意味は角周波数 角振動数 や角速度や化学構造の位置を表す Wやwの書き方 書き順 は Wみたいな記号の大文字と小文字 ウルトラフリーダム




電気回路の角周波数wの意味は Yoshihiraのスペース




高校数学 高次式の値 方程式を利用した次数下げ 受験の月




Okra ただ このまま終わるのはなんだかもったいない 1の3乗根w オメガ を載せちゃったやつです 数学が得意な子にもたくさん発見があるワークブックになるといいな



1の三乗根オメガを用いた計算と因数分解 高校数学の美しい物語



1の三乗根wは複素平面で見るとすぐ分かる ばたぱら



1



数学のwとはなんですか 性質と使うときを教えてくれる方いま Yahoo 知恵袋



数学についてです W オメガ とゆうのが本当に意味が分 Yahoo 知恵袋




1の三乗根のうち 虚数のものをwとする Wバー W 2を示せ Clear




Kw キロオーム とw オーム の換算 変換 方法 1kw キロオーム は何w オーム 1w オーム は何kw キロオーム 白丸くん



1の三乗根wは複素平面で見るとすぐ分かる ばたぱら



ある数学のサイトを見ていて思ったのですが このオメガの上のバーは Yahoo 知恵袋




勉強しよう数学 複素数平面のグラフの変換方法




2ページ目 Blにおける オメガバースの事情 アニメイト編集部bl塾 応用編 アニメイトタイムズ




学校の先生には オメガの二乗は共約な複素数だから 値はオメガと変わらないし 計算して Clear




複素数と方程式 1の3乗根の性質について 日々是鍛錬 ひびこれたんれん



香川大学 法学部 10年問題3 Suugaku Jp
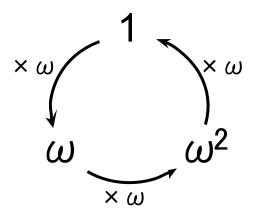



1の3乗根 高校数学の無料オンライン学習サイトko Su




数学 でwを習ったのですが あまりよくわかりません 教えてください Clear
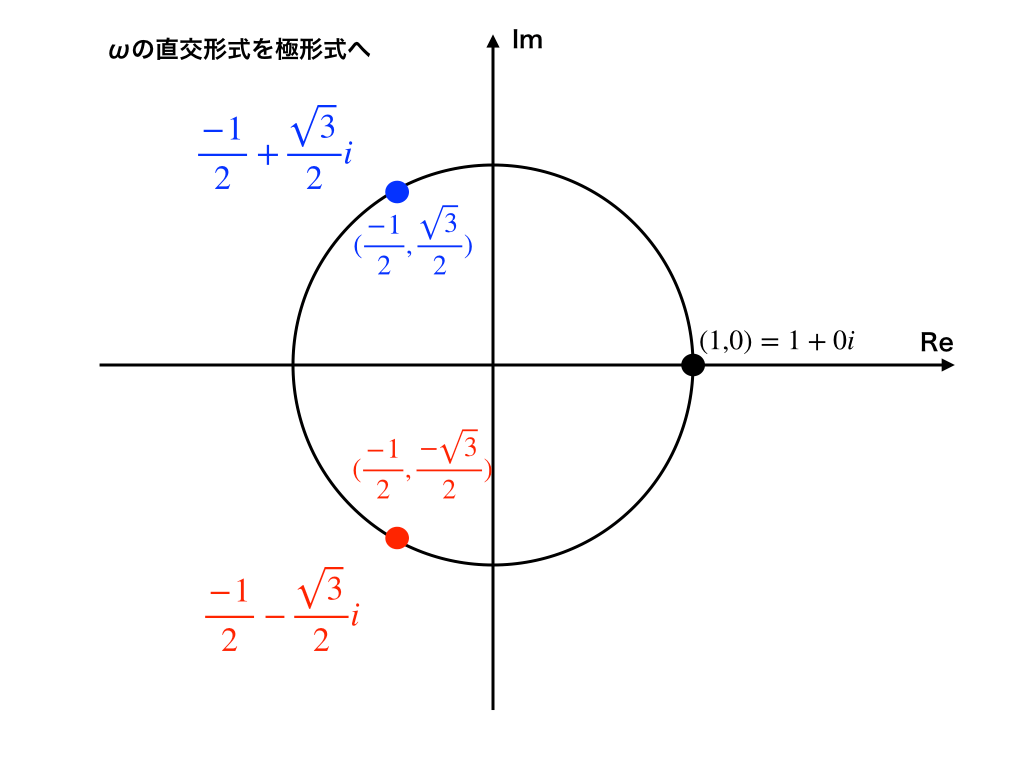



オメガ Wの意味と計算のコツ 複素数平面上での意味をわかりやすく




Df Twitterren 1 の虚数立方根 W の使用方法は W 2 W 1 0 と W 3 1 だけではない Http T Co Echtjjpkbi




W オメガ の計算 やり方はどうする 計算手順をていねいに解説するぞ 数スタ




W オメガ の計算 やり方はどうする 計算手順をていねいに解説するぞ 数スタ
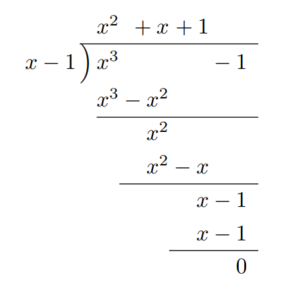



1の3乗根 オメガ W をなるべくわかりやすく解説してみる 高校数学の知識庫



高2数学92についてです なんとなく解いて正解したものもあるのですが Yahoo 知恵袋



ある数学のサイトを見ていて思ったのですが このオメガの上のバーは Yahoo 知恵袋




数学 複素数と方程式 W オメガ の計算 高校生が数学のテストの前に見る授業 Youtube




高校数学 1の3乗根 虚数立方根 Wの性質 X X 1で割ったときの余り 受験の月




1の立方根 3乗根 のw オメガ の性質と関係式の使い方




高校物理 角速度 W 映像授業のtry It トライイット




角速度の公式と求め方 見やすいイラストで一発理解 計算問題付き 高校生向け受験応援メディア 受験のミカタ



数学最強キャラ考察スレ 考えられる限りの 最大に巨大な物体を作る 到達不能基数 可測基数 コンパクト基数 巨大基数 クラスへ



0 件のコメント:
コメントを投稿