Z平方根の加減 zいろいろな計算 *「ページ表示」を「見開き」でご覧いただきますと、問題とその 答えが見やすくなります。 *このテキストは家庭学習の補助教材としてのみご利用いただけま す。その他(問題の改変、商用など)の利用はご遠慮ください 平方根の利用③ 問題はこちらです。 直径が30cmの丸太から、切り口ができるだけ大きな正方形となるように角材をとる。 このとき次の問いに答えよ。 (1)正方形の面積を求めよ。 解答と解説は1番下にあります。 問題中にある青字のリンクをタップ練習問題の解説動画はこちら!≪ Coming Soon ≫ 解説動画①≪ Coming Soon ≫ Twitterhttps//twittercom/Laf_academy Instagramhttps//wwwinstagram

二次方程式の解き方 平方根の知識を使う問題のパターン 中学や高校の数学の計算問題
平方根問題 応用
平方根問題 応用-商品説明 商品内容 DVD+プリント(B4サイズ) 3-2 平方根 応用編 プリント16枚 DVD80分 *自分でも解いてみる形式ですので、実際の学習時間は 収録時間の2倍~3倍程度です。 他単元ごとに多数販売しております。 講師紹介 大学在籍中4年間、個別指導塾講師、塾講師、模試採点など 教育関連の 平方根で教えて欲しい問題があります √5cmは面積が5cm^2の正方形の1辺の長さであるこのことを利用して下の正方形ABCDの長さ√5cmの線分をかけ という問題です 三平方の定理を使えば分かるんですが、平方根までの知識で解く方法が分かりません 回答は点を結んで出来る四角形です




平方根の応用 不等式 算数 数学が好きになりmath
平方根の計算の応用 √の計算の四則計算や、√が含まれる2乗の展開、計算の応用問題について学習します。 根号の計算の応用 根号の平方完成 平方根の計算の応用 平方根の計算の応用 平方根の計算の応用 平方根の計算の応用 平方根の計算の応用±を忘れないように注意! なぜ±が必要?と思った人はアオイゼミの授業動画でチェック! それでは応用です。 先ほどの動画の問題を解いてみましょう。 平方根の性質と応用問題 中学生数学特訓プラン 基礎力養成特訓プラン 推奨学年中学1年~中学3年生内容計算の基礎養成演習時間割50分授業×週1回授業回数月間4回授業料中学1年生:8,300円中学2年生
FdData 中間期末:中学数学3 年:平方根2 乗法・除法/平方根の近似値/加法・減法/加減乗除全般/式の値/ 平方根の応用(√が整数) /平方根の応用(整数部分・小数部分)/平方根の応用(その他)/ FdData 中間期末製品版のご案内 FdData 中間期末ホーム ここからは、この平方根の小数部分についての計算式を、工夫して解く方法をご紹介します。 このように、3乗の式があるような複雑な問題の場合は、値を代入していって、徐々に係数を下げていく方法が有効な場合があります。 (星光学院高校) a a は2練習問題の解説動画はこちら!≪ Coming Soon ≫ 解説動画①中3数学よくわかる 素因数分解!!!https//youtube/JAbtSH0zGLo 解説
3年生数学 平方根の応用問題 テーマ「平方根の応用問題」 ☆範囲 教科書p64~65 → ワーク39 a,b ※教科書は読むだけでよい(平方根は実は身の回りにたくさんあるよーってこと) ※ワークは入試を意識した平方根の応用問題である。挑戦しよう。平方根(代入) 次の問いに答えよ ① x= √ 71 のときx 2 2x1の値を求めよ。 ② x= √ 6 5のとき x 210xの値を求めよ。 ③ x= √ 53 のときx 2 6x2の値を求めよ。 xy= √ 13, xy=3のとき次の問いに答えよ。 ① (xy) 2 の値を求めよ。 ② x 2 y 2 の値を求めよ。 ③ x 2 5xyy 2 の値を求めよ。 というわけで、今回の記事では平方根の利用問題について解説していきます。 平方根の利用問題とは ルートが自然数となるようにするためには、何を掛ければよいか? 直径㎝の丸太から、できるだけ大きな正方形を作るにはどうする? 1辺の長さが




中3 基礎 平方根が苦手な方へ 中3数学 中学生 数学のノート Clear




中3数学 ルートの計算とカッコ カッコの公式 練習編 映像授業のtry It トライイット
サンプル(数学中学3年) 会員版では高校入試問題を詳細に解説しています。 平方根 根号の計算 中学3年生 平方根で周りに差をつけられます! 平方根 問題 応用問題 応用 中3 このノートが参考になったら、著者をフォローをしませんか? 気軽に新しいノートをチェックすることがでこんにちは、あすなろスタッフのカワイです。 今回は平方根の問題演習です。 全部解くことが出来たら、この単元を十分理解していると言っても過言ではありません! もし出来ない問題があっても、分からない問題について復習できるペー



中3 平方根の頻出計算問題を解く その2 上北沢 哲英会 個人塾 連絡用ブログ



平方根とは 計算方法や求め方 近似値の覚え方 利用問題 受験辞典
平方根の応用問題(代入)4 解説 次の問に答えなさい。 (1) ab=2 7, ab=2 のとき a 2abb 2 の値を求めよ。 (2) xy=3 5, xy=4 のときx 2 y 2 の値を求めよ。 (3) xy=2 3, xy=2 のときx 2 xyy 2 値 今回は、前回までで触れられなかった平方根の問題をあつかう。 前回←平方根の利用(範囲を満たす平方根) 次回→2次方程式の解き方(基) 24 平方根の利用 241 整数・自然数になるようにする(標~難) 242 整数部分,小数部分(標~難) 243 不等式と平方根(標~難) 平方根の大小関係と大小比較の練習問題|中学数学 平方根の大小問題の基本~標準レベル − √ 2 − 2 、 − √ 5 − 5 、 − √ 7 − 7 の大小関係を不等号で表せ。 解説 数直線上で表わすと、それぞれこのようになります。 a < b < c a < b < c のとき −




中学3年 平方根 第12講 清水塾




有理化とは やり方を分かりやすく解説 練習問題つき 高校生向け受験応援メディア 受験のミカタ
こんにちは、すもきちです。 平方根の解説記事もこれで最後になります。 苦手な人も多そうなこの平方根の単元ですが、最後に応用問題の解説をします。 実際に入試に出るような問題を取り扱いますが、分かりやすく解説するので苦手な人でも理解できるはずです。 今回は、前回に引き続き計算問題を見ていく。 ただし、今回は少しむずかしいレベルを扱う。 前回←平方根の計算(基) 次回→平方根の利用(標~難) 21 平方根の基本と練習問題(基) 22 計算への準備と平方根の性質(基) 23 平方根の計算 231 平方根の計算と四則計算・展開・式の値(基)平方根応用(図形)1,2,3 解説 1 図の abcはab=ac,∠bac=90°の 直角二等辺三角形である。 頂点aから辺bcに垂線をおろしその交点をpとする。 ap=2cm, bc=4cmのとき次の問いに答えよ。 (1) abcの面積を求めよ。 (2)辺abの長さを求めよ。 a b c p (1) 底辺をbcとすると、高さがap




中3平方根の応用問題です 解説と解き方教えてください Clear




中学数学3年 素因数分解の応用 約数の個数 平方数 受験の月
平方根を利用した図形問題は様々にあります。 例えば、このような問題は平方根の記号に関する基本的な理解をつかわなければなりません。 一辺がxの正方形の面積が10のとき、xを求めよ。 このような問題の場合 2乗して10になる自然数は何ですか?練習問題の解説動画はこちら!≪ Coming Soon ≫ 解説動画①平方根を a√b に書き換え!~√の中身が整数~中3数学httpsなどと覚えることがあるので, から直接, と答えてもよい. しかし,それ以上大きい数の平方根, などの値は通常覚えないので,様々な問題に対応できるようにするためには,上記の答案のように2乗して考えるのがよい.




一次関数 変域の問題 中学数学 練習問題プリント 数奇な数




平方根 ルートとは 平方根の求め方を解説 分数や小数の場合はどうやる 数スタ
今回は平方根の利用問題を見ていく。 特に詰まりやすいところなので、ゆっくりとやっていこう。 前回←平方根の計算(標~難) 次回→平方根の利用(2)整数部分小数部分(標~難) 24 平方根の利用 241 整数・自然数になるようにする(標~難) 242 整数部分,小数部分(標~難)平方根 整数部分・小数部分1 無料で使える中学学習プリント http//chugakumanabihirobanet/ 2 解答 ① 2 2より よって整数部分は 中3数学 平方根の利用 式の値⑩(応用レベル) 中3数学 平方根の利用 式の値⑩ 応用レベル 今回の問題はこちら x=√3+√2、 y=√3ー√2のとき、 y/x ー x/y の値を求めなさい。 解説は下にあります。 "中3数学 平方根の利用 式の値⑩(応用レベル



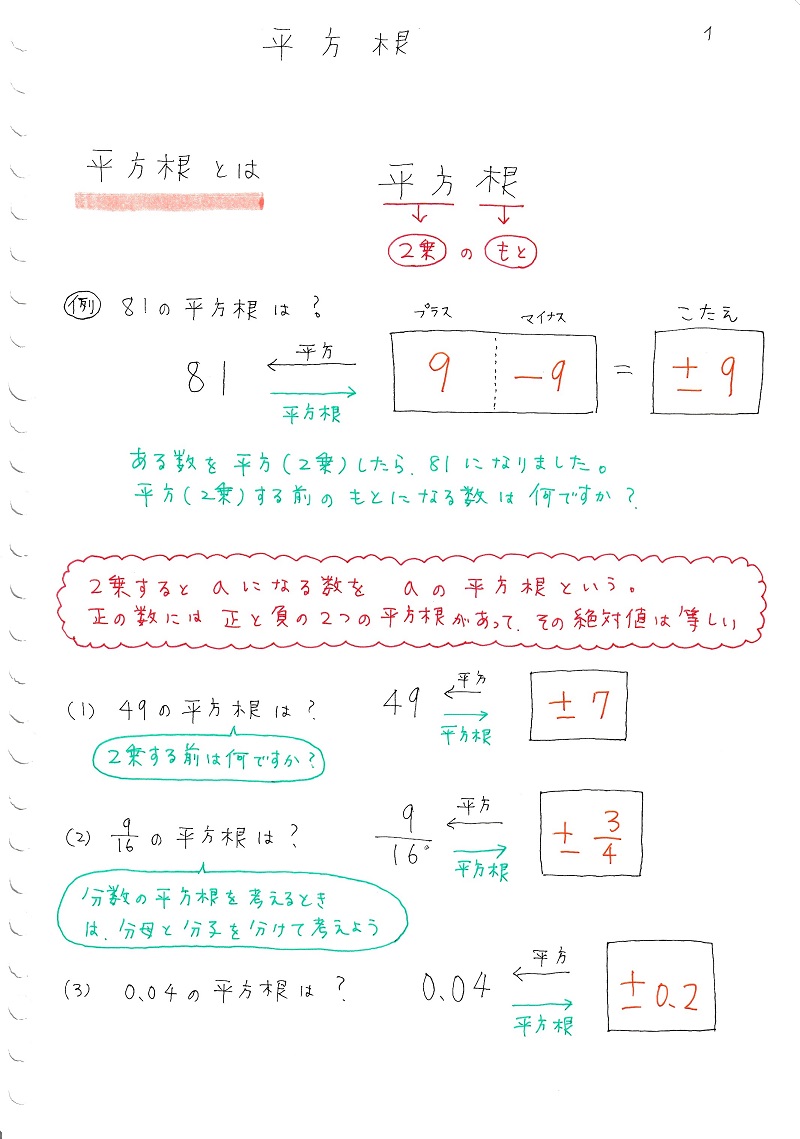
1




世界一わかりやすい数学問題集中3 2章 平方根
平方根の応用(整数部分・小数部分) no2 /5 z √7 −1 6 +4y √10 +4 y− 平方根 整数部分・小数部分2平方根応用 (図形) 図の ABCはAB=AC,∠BAC=90°の直角二等辺三角形である。 頂点Aから辺BCに垂線をおろしその交点をPとする。 AP=2cm, BC=4cmのとき次の問いに答えよ。 ABCの面積を求めよ。 辺ABの長さを求めよ。Amazoncojp: 中学 数学 3年応用問題集 2 平方根 DVD (授業テキスト問題集)"プロ家庭教師が教える" 中学生用学習DVD 中学受験 予習 復習 試験対策 DVDROM DVD



中学数学 平方根 ママ塾ノート
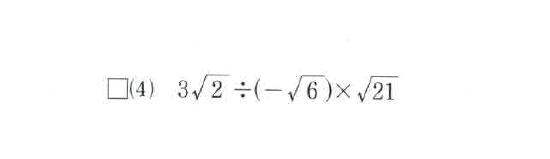



6月21日更新 中3一斉授業 数学 平方根の応用問題 成績 上がってます 根城学習塾 八戸市
平方根 平方根(1) 問題一括 (8,085Kb) 解答一括 (9,324Kb) 平方根(2) 平方根の大小 有理数と無理数 平方根の乗法 平方根の除法 平方根の性質(1) 平方根の性質(2) 平方根の近似値 根号を含む計算 有理化 平方根の加法・減法(1) 平方根の加法・減法(2) 平方根の 平方根の利用③ 中学3年 数学 平方根の利用③ 問題はこちらです。 問題 直径が30cmの丸太から、切り口ができるだけ大きな正方形となるように角材をとる。 このとき次の問いに答えよ。 (1)正方形の面積を求めよ。 (2)正方形の1辺を根号を用いて平方根の計算の応用 今回は、数学のブログである。 平方根の計算で大事なるのは、「平方数」ならば、ルートを外せるという事である。 平方数とは0と1以外の数は全て偶数乗になる数の事である。 では、其れを踏まえ、以下の問題を解いてみよう。




無料 中3数学 発展 応用問題 問題プリント 311 平方根3 平方根の性質




Amazon Co Jp 中学 数学 3年 基礎 問題集 2 平方根 Dvd 授業 テキスト 問題集 プロ家庭教師が教える 中学生用学習dvd 中学受験 予習 復習 試験対策 Dvd Rom Pcソフト



U9j580gf8iba369ji2w Xyz P 599




平方根の式の値 無料で使える中学学習プリント




平方根 を自然数にするとき の問題の解き方 現役塾講師のわかりやすい中学数学の解き方




中3 平方根 応用問題 やや難問に挑戦 をストップモーションで Youtube




Amazon Co Jp 中学 数学 3年 応用 問題集 2 平方根 Dvd 授業 テキスト 問題集 プロ家庭教師が教える 中学生用学習dvd 中学受験 予習 復習 試験対策 Dvd Rom Pcソフト




中学3年生 数学 平方根の加法 減法 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




平方根 応用問題 19 N が自然数になるときの N の値 中3数学 Youtube




中学数学 平方根 のコツ 平方根とは 平方根の大小




世界一わかりやすい数学問題集中3 2章 平方根




平方根の応用問題 難問までジャンル別一覧 中学数学から高校入試問題まで 坂田先生のブログ



1




平方根の応用 不等式 算数 数学が好きになりmath




70以上 5 の 平方根 シモネタ




無料 中3数学 発展 応用問題 問題プリント 310 平方根2 大小




数学 中3 23 ルートの問題をつめこんでみた Youtube




平方根 応用問題 中学数学 練習問題プリント 数奇な数
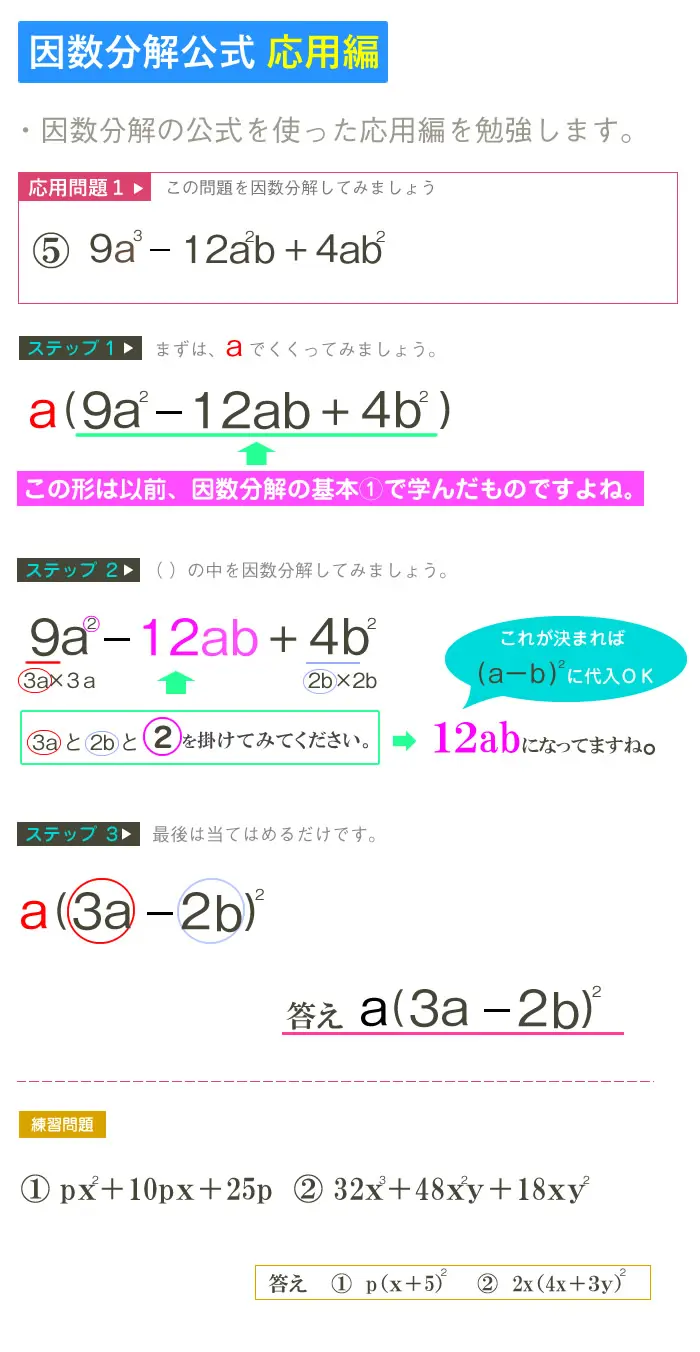



因数分解の応用編1 看護学校の受験数学 中学数学 を分かりやすく図解で説明 Kazアカデミー 大阪の看護学校 看護予備校




中3 平方根 特別編 正誤問題 中学数学の勉強に



中学数学到達度テスト集中3前期 多項式 平方根 2次方程式 2次関数 Gakurin1345 学林舎 通販 Yahoo ショッピング




この問題解ければすごい 平方根と自然数の応用問題 中学数学 理科 寺子屋塾の復習サイト




数学問題集の部屋 平方根の計算 入試問題1の解答



Sukinakazu Net Niji Houteisiki Niji Houteisiki Pdf




平方根の利用 清水塾




平方根の計算 平方根のチョー簡単な問題をまとめたよ 三重の個人契約家庭教師




ルート計算 展開公式をつかう3つの平方根問題の解き方 Qikeru 学びを楽しくわかりやすく



1




数学の学習ノート 中学校教材 数学 教科書対応ワーク 株式会社正進社 教育図書教材の出版




指数法則を使う問題の計算練習 高校数学の知識庫



平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス



平方根の割り算は 1分でわかる計算 割り算の問題とやり方 有理化 分数との関係



3 45第2章平方根の応用 平方根の性質を使った問題 フロントエンドなブログ




中3数学 平方根の大小関係 練習編 映像授業のtry It トライイット




中学3年生 数学 平方根 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



平方根応用 図形




平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ
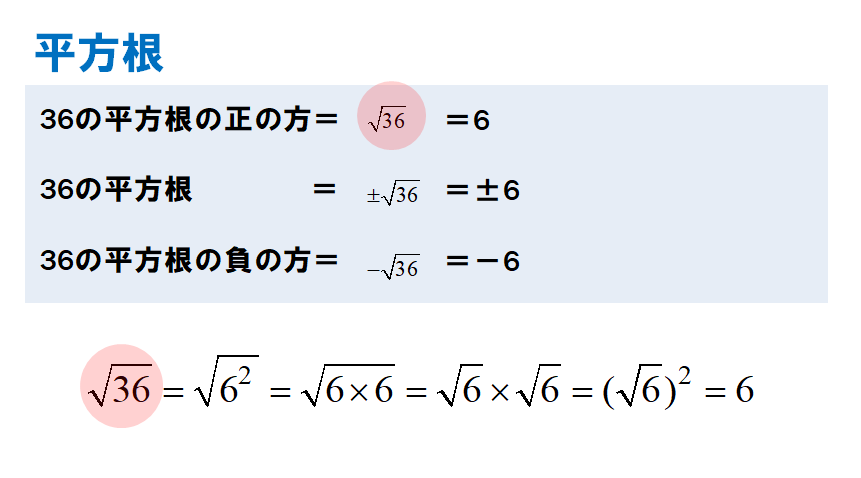



中3数学 平方根の性質の定期テスト対策問題 Examee




中3 数学 平方根問題 応用 慣れれば無双も夢じゃない 授業動画あり アオイのホームルーム



無料 中2数学 応用 発展問題 問題プリント 310 平方根2 大小



3 39第2章平方根の計算 平方根の加法減法 応用編




Paypayフリマ プロが教える 数学 中学 3年 Dvd 2 平方根 応用編 問題集




最も選択された 平方根 の 利用 問題 ニスヌーピー 壁紙




平方根の大小関係と大小比較の練習問題 難易度別に解説 坂田先生のブログ




中学数学 平方根の利用 ママ塾ノート



1




Paypayフリマ プロが教える 数学 中学 3年 Dvd 2 平方根 基礎編 問題集




素因数分解を利用する応用問題の解き方 現役塾講師のわかりやすい中学数学の解き方




1日一問 平方根の応用問題 中学数学 理科 寺子屋塾の復習サイト




中3平方根の応用問題です 解き方と解説教えてください Clear




二次方程式の解き方 少しだけ応用した平方根の問題 中学や高校の数学の計算問題




無料 中3数学 発展 応用問題 問題プリント 312 平方根4 乗法 除法2




平方根 ルートnをaルートbの形に変える方法 中学数学 定期テスト対策サイト




中3数学 平方根 平方根の応用問題 Youtube




無料 中3数学 発展 応用問題 解答プリント 312 平方根4 乗法 除法2




平方根 ルート の重要な計算方法まとめ 数学fun




ベストコレクション 平方根 の 利用 平方根の利用 問題集 Nyosspixm3db




平方根の計算 やり方は をつけてルートをつけよう 中学や高校の数学の計算問題
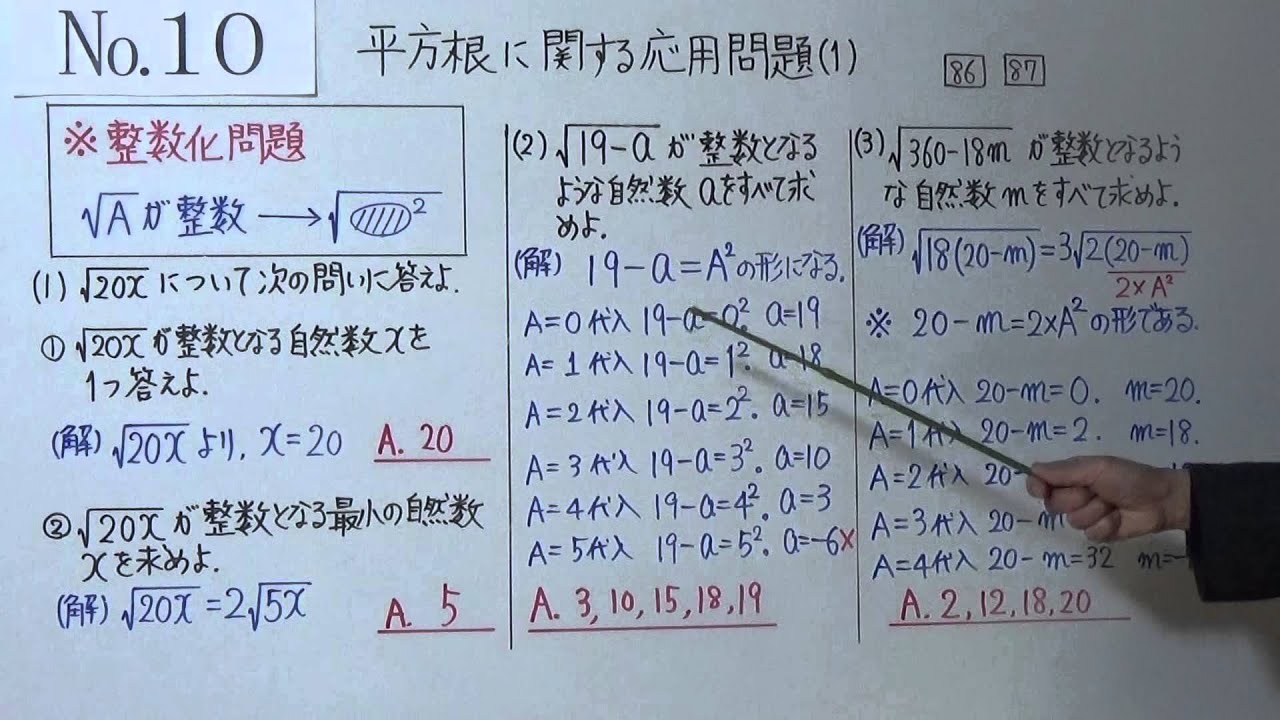



中3 10 1 平方根の応用 整数化問題 Youtube




無料 中3数学 発展 応用問題 問題プリント 314 平方根6 いろいろな計算1



方程式の応用問題 平方根との混合問題 中学数学の方程式 中間 期末テスト 高校入試対策




中3 数学 平方根の利用 この問題の解説をお願いします 整数部分と少数 Okwave




中3 数学 板書 平方根 中学生 数学のノート Clear




数学 質問解答 平方根の利用 の わかりやすい 考え方 解き方はこちらです 文章題 平方根 中3 中学数学 質問ありがとうございました 行間 ぎょうのあいだ 先生




平方根の利用 清水塾




平方根の利用 正方形の対角線 丸太 自然数を求める解き方は いろんな利用問題を解説 中学数学 理科の学習まとめサイト




平方根 の勉強法のわからないを5分で解決 映像授業のtry It トライイット




平方根 計算 応用問題 中学数学 練習問題プリント 数奇な数



授業実践記録




2次方程式の応用問題の解き方 文章問題 数学fun




ルートの応用問題 を変形して 計算できるようにする 中学や高校の数学の計算問題




平方根の応用 無料で使える中学学習プリント




可能性を考える 平方根の 問題 名寄 算数数学教室より




中学3年 平方根 第11講 清水塾




中3数学 平方根 19 中学数学高校数学個別指導in山形市 数専ゼミ




この問題を教えていただきたいです Clear
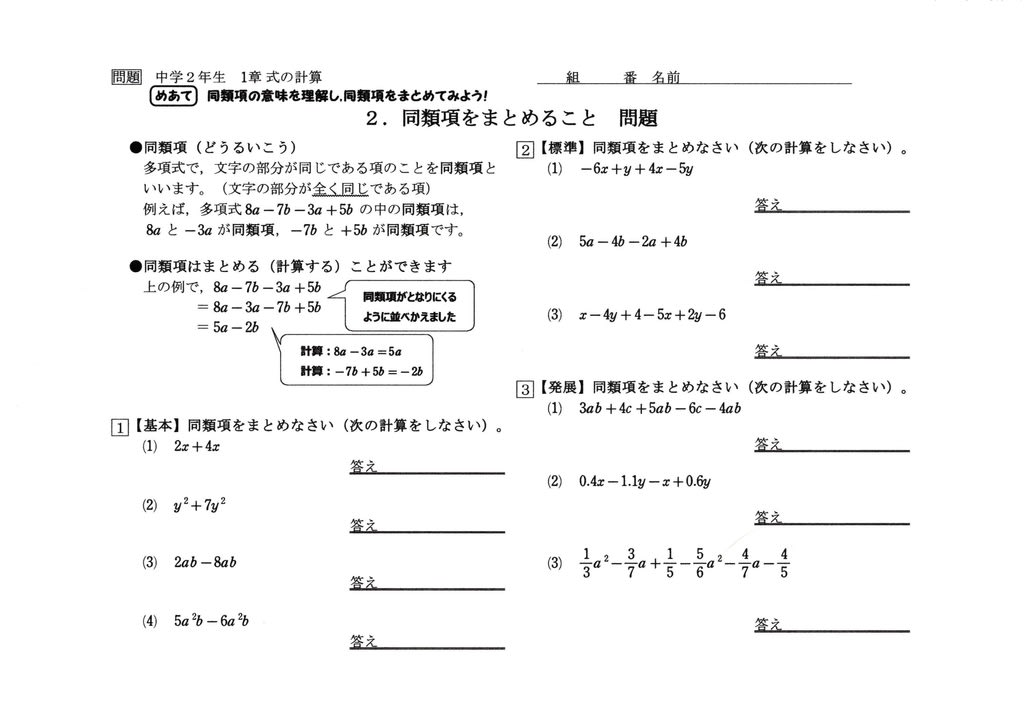



中2 式の計算2 同類項をまとめること 予習 中学数学の勉強に




中学3年生 数学 平方根のいろいろな計算 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




全問題 無料学習プリント教材




この問題を教えていただきたいです Clear



3 46第2章平方根の応用 平方根の性質を使った問題 2 フロントエンドなブログ




6月21日更新 中3一斉授業 数学 平方根の応用問題 成績 上がってます 根城学習塾 八戸市



中学3年 平方根 応用問題 テスト前の復習にどうぞ 学びの森




無料 中3数学 発展 応用問題 解答プリント 311 平方根3 平方根の性質




中学数学3年 2次方程式 平方根の利用 受験の月




高校数学 平方根の定義と2乗の平方根 A の基本的な扱い 受験の月




中学数学 平方根 整数になる自然数n の簡単なやり方 丁寧な解説 スタディーランナップ




二次方程式の解き方 平方根の知識を使う問題のパターン 中学や高校の数学の計算問題




平方根の応用 無料で使える中学学習プリント



平方根の割り算は 1分でわかる計算 割り算の問題とやり方 有理化 分数との関係



0 件のコメント:
コメントを投稿